RESEÑA HISTÓRICA
LECTURA Y BÚSQUEDA DE LA INFORMACIÓN HISTÓRICA DE LA EVOLUCIÓN DE RELACIÓN Y FUNCIÓN
El concepto de función como un objeto matemático independiente, susceptible de ser estudiado por sí solo, no apareció hasta los inicios del cálculo en el siglo XVII. Rene Descartes, Isaac Newton y Gottfried Leibniz establecieron la idea de función como dependencia entre dos cantidades variables. Leibniz en particular acuñó los términos «función», «variable», «constante» y «parámetro». La notación f(x) fue utilizada por primera vez por A.C. Clairaut, y por Leonhard Euler en su obra Commentarii de San petersburgo en 1736.
Inicialmente, una función se identificaba a efectos prácticos con una expresión analítica que permitía calcular sus valores. Sin embargo, esta definición tenía algunas limitaciones: expresiones distintas pueden arrojar los mismos valores, y no todas las «dependencias» entre dos cantidades pueden expresarse de esta manera. En 1837 Dirichlet propuso la definición moderna de función numérica como una correspondencia cualquiera entre dos conjuntos de números, que asocia a cada número en el primer conjunto un único número del segundo.
La intuición sobre el concepto de función también evolucionó. Inicialmente la dependencia entre dos cantidades se imaginaba como un proceso físico, de modo que su expresión algebraica capturaba la ley física que correspondía a este. La tendencia a una mayor abstracción se vio reforzada a medida que se encontraron ejemplos de funciones sin expresión analítica o representación geométrica sencillas, o sin relación con ningún fenómeno natural; y por los ejemplos «patológicos» como funciones continuas sin derivada en ningún punto.
Durante el siglo XIX Julius Wilhelm Richard Dedekind, Karl Weierstrass, Georg Cantor, partiendo de un estudio profundo de los números reales, desarrollaron la teoría de funciones, siendo esta teoría independiente del sistema de numeración empleado. Con el desarrollo de la teoría de conjuntos, en los siglos XIX y XX surgió la definición actual de función, como una correspondencia entre dos conjuntos de objetos cualesquiera, no necesariamente numéricos. También se asoció con otros conceptos vinculados como el de relación binaria.
PAR ORDENADOS
Un par ordenado es una pareja de objetos matemáticos, en la que se distingue un primer elemento y un segundo elemento. El par ordenado cuyo primer elemento es a y cuyo segundo elemento es b se denota como (a, b).
Un par ordenado (a, b) no es el conjunto que contiene a a y b, denotado por {a, b}. Un conjunto está definido únicamente por sus elementos, mientras que en un par ordenado el orden de estos es también parte de su definición. Por ejemplo, los conjuntos {0, 1} y {1, 0} son idénticos, pero los pares ordenados (0, 1) y (1, 0) son distintos.
Los pares ordenados también se denominan 2-tuplas o vectores 2-dimensionales. La noción de una colección finita de objetos ordenada puede generalizarse a más de dos objetos, dando lugar al concepto de n-tupla.
El producto cartesiano de conjuntos, las relaciones binarias, las coordenadas cartesianas, las fracciones y las funciones se definen en términos de pares ordenados.

La propiedad característica que define un par ordenado es la condición para que dos de ellos sean idénticos:
|
Los elementos de un par ordenado también se denominan componentes.
PRODUCTO CARTESIANO
Dados dos conjuntos X e Y, la colección de todos los pares ordenados (x, y), formados con un primer elemento en X y un segundo elemento en Y, se denomina el producto cartesiano de X e Y, y se denota X × Y. El producto cartesiano de conjuntos permite definir relaciones y funciones.
Generalizaciones
Es habitual trabajar con colecciones ordenadas de más de dos objetos, sin más que extender la definición del par ordenado. Por ejemplo, un trío ordenado o terna ordenada es una terna de objetos matemáticos en la que se distinguen un primer, segundo y tercer elemento. La propiedad principal de un trío ordenado es entonces:
En general se puede adoptar una definición similar para un número cualquiera de elementos n, dando lugar así a una n-tupla.
Construcción
La condición de igualdad entre pares ordenados es su única propiedad matemática relevante. Sin embargo, en teoría de conjuntos se construyen todos los objetos matemáticos a partir de conjuntos: números, funciones, etc. En este contexto, se define par ordenado como un conjunto particular de tal manera que su relación de igualdad sea la correcta.
La definición conjuntista habitual, debida a Kuratowski, es:
Mediante el axioma de extensionalidad y el axioma del par puede demostrarse que este término define un conjunto, con la propiedad característica del par ordenado.
Construcciones alternativas
La definición conjuntista de Kuratowski no es la única existente en la literatura matemática:
PRODUCTO CARTESIANO DE CONJUNTOS
El producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par ordenado del primer conjunto y el segundo elemento del par ordenado del segundo conjunto.
Por ejemplo, dados los conjuntos:
y
su producto cartesiano es:
que se representa:
El producto cartesiano recibe su nombre de René Descartes, cuya formulación de la geometría analítica dio origen a este concepto.
Un par ordenado es una colección de dos objetos distinguidos como primero y segundo, y se denota como (a, b), donde a es el «primer elemento» y b el «segundo elemento». Dados dos conjuntos A y B, su producto cartesiano es el conjunto de todos los pares ordenados que pueden formarse con estos dos conjuntos:
|
Puede definirse entonces el cuadrado cartesiano de un conjunto como A2 = A × A.
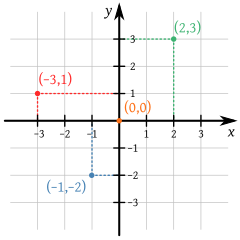
Pintura y pinceles (0, +1), (0, −1), (0, +2), ..., (+1, 0), ... (−1, 0), ... }, es decir, el conjunto de los pares ordenados cuyas componentes son enteros. Para representar los números enteros se utiliza la recta numérica, y para representar el conjunto Z2 se utiliza un plano cartesiano (en la imagen).
Sean los conjuntos T de tubos de pintura, y P de pinceles:
El producto cartesiano de estos dos conjuntos, T × P, contiene todos los posibles emparejamientos de pinceles y tubos de pintura. De manera similar al caso de un plano cartesiano en el ejemplo anterior, este conjunto puede representarse mediante una tabla:
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
Generalizaciones
Caso finito
Dado un número finito de conjuntos A1, A2, ..., An, su producto cartesiano se define como el conjunto de n-tuplas cuyo primer elemento está en A1, cuyo segundo elemento está en A2, etc.
|
Puede definirse entonces potencias cartesianas de orden superior a 2, como A3 = A × A × A, etc. Dependiendo de la definición de n-tupla que se adopte, esta generalización puede construirse a partir de la definición básica como:
o construcciones similares.
Caso infinito
En el caso de una familia de conjuntos arbitraria (posiblemente infinita), la manera de definir el producto cartesiano consiste en cambiar el concepto de tupla por otro más cómodo. Si la familia está indexada, una aplicación que recorra el conjunto índice es el objeto que distingue quién es la «entrada k-ésima»:
|
donde ∪F denota la unión de todos los Ai. Dado un j ∈ I, la proyección sobre la coordenada j es la aplicación:
En el caso de una familia finita de conjuntos {A1, ..., An} indexada por el conjunto In = {1, ..., n}, según la definición de n-tupla que se adopte, o bien las aplicacionesf : In → ∪i Ai de la definición anterior son precisamente n-tuplas, o existe una identificación natural entre ambos objetos; por lo que la definición anterior puede considerarse como la más general.
Sin embargo, a diferencia del caso finito, la existencia de dichas aplicaciones no está justificada por las hipótesis más básicas de la teoría de conjuntos. Estas aplicaciones son de hecho funciones de elección cuya existencia sólo puede demostrarse en general si se asume el axioma de elección. De hecho, la existencia de funciones de elección (cuando todos los miembros de F son no vacíos) es equivalente a dicho axioma.
Propiedades
El conjunto vacío actúa como el cero del producto cartesiano, pues no posee elementos para construir pares ordenados:
|
El producto cartesiano de dos conjuntos no es conmutativo en general, salvo en casos muy especiales. Lo mismo ocurre con la propiedad asociativa.
|
Puesto que el producto cartesiano puede representarse como una tabla o un plano cartesiano, es fácil ver que el cardinal del conjunto producto es el producto de los cardinales de cada factor:
|
En teoría de conjuntos, la fórmula anterior de cardinal del producto cartesiano como producto de los cardinales de cada factor, sigue siendo cierta utilizando cardinales infinitos.
RELACIÓN
Una relación binaria es una relación entre dos conjuntos.
El concepto de relación implica la idea de enumeración, de algunos de los elementos, de los conjuntos que forman tuplas.
Un caso particular es cuando todos los conjuntos de la relación son iguales:  en este caso se representa
en este caso se representa  como
como  , pudiéndose decir que la relación pertenece a A a la n.
, pudiéndose decir que la relación pertenece a A a la n.
 en este caso se representa
en este caso se representa  como
como  , pudiéndose decir que la relación pertenece a A a la n.
, pudiéndose decir que la relación pertenece a A a la n.

- DOMINIO DE UNA RELACIÓN

- El dominio (conjunto de definición o conjunto de partida) de una función
 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 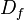 . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío. - Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina imagen de esa función.
Definición
El dominio de definición de una función f:X→Y se define como el conjunto X de todos los elementos x para los cuales la función f asocia algún y perteneciente al conjunto Y de llegada, llamado codominio. Esto, escrito de manera formal:
Propiedades
Dadas dos funciones reales: Se tienen las siguientes propiedades:
Se tienen las siguientes propiedades:Cálculo del dominio de una función
Para el cálculo certero del dominio de una función, se debe introducir el concepto de restricción en el cuerpo real. Estas restricciones ayudarán a identificar la existencia del dominio de una función. Las más usadas son:Raíz n-ésima de f(x)
No existe restricción si n es impar, pero si n es par, la función f(x) necesariamente deberá ser mayor o igual que cero, ya que las raíces negativas no están definidas en el cuerpo real. Por ejemplo:El índice de la raíz es par (2), por tanto ; despejando, se tiene que x ≥ 3. El dominio entonces será el conjunto de todos los reales en el intervalo [3,+∞).
; despejando, se tiene que x ≥ 3. El dominio entonces será el conjunto de todos los reales en el intervalo [3,+∞).Logaritmo de f(x)
La restricción está al estudiar las propiedades de los logaritmos las cuales dicen que estos no están definidos para números negativos, por tanto toda función contenida dentro de un logaritmo debe ser necesariamente mayor estricto de cero. Por ejemplo:Por la propiedad anteriormente citada, se observa que para que esta función exista, necesariamente ; despejando, se obtienen dos soluciones
; despejando, se obtienen dos soluciones  y
y  . La unión de ambas soluciones representa el dominio de la función, que está definida como el conjunto (-∞, -3) U (3, +∞).
. La unión de ambas soluciones representa el dominio de la función, que está definida como el conjunto (-∞, -3) U (3, +∞).Fracciones
Otras propiedades de las matemáticas pueden ayudar a obtener el dominio de una función y excluir puntos donde esta no esté definida, por ejemplo, una función que tenga forma de fracción no estará definida cuando el denominador valga cero, ya que esto es una indeterminación.Ejemplos
Algunos dominios de funciones reales de variable real: El dominio de esta función, así como el de cualquier función polinómica y exponencial, es
El dominio de esta función, así como el de cualquier función polinómica y exponencial, es  .
.
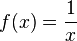 El dominio de esta función es
El dominio de esta función es  puesto que la función no está definida para x = 0.
puesto que la función no está definida para x = 0.
 El dominio de esta función es
El dominio de esta función es  ya que los logaritmos están definidos sólo para números positivos.
ya que los logaritmos están definidos sólo para números positivos.
 El dominio de esta función es
El dominio de esta función es 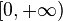 porque la raíz de un número negativo no existe en el cuerpo de los reales.
porque la raíz de un número negativo no existe en el cuerpo de los reales.
- RANGO DE UNA RELACIÓN

- la imagen (conocida también como campo de valores o rango) de una función
 es el conjunto formado por todos los valores que puede llegar a tomar la función. Se puede denotar como
es el conjunto formado por todos los valores que puede llegar a tomar la función. Se puede denotar como 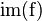 ,
,  o bien
o bien  y formalmente está definida por:Adicionalmente, es posible hablar de la imagen de un elemento (del dominio) para hacer referencia al valor que le corresponde bajo la función. Esto es, si
y formalmente está definida por:Adicionalmente, es posible hablar de la imagen de un elemento (del dominio) para hacer referencia al valor que le corresponde bajo la función. Esto es, si es una función, entonces la imagen del elemento
es una función, entonces la imagen del elemento 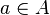 es el elemento
es el elemento  .
.Diferencia con el contra-dominio
Si es una función, al conjunto Y de valores que podría tomar la función se conoce como contra-dominio, mientras que el conjunto imagen consta únicamente de los valores que realmente toma.Es importante diferenciar el concepto de contra-dominio del concepto de conjunto imagen.Por ejemplo, la función
es una función, al conjunto Y de valores que podría tomar la función se conoce como contra-dominio, mientras que el conjunto imagen consta únicamente de los valores que realmente toma.Es importante diferenciar el concepto de contra-dominio del concepto de conjunto imagen.Por ejemplo, la función tiene por contra-dominio el conjunto de todos los números reales, pero como nunca toma realmente valores negativos, el conjunto imagen está formado únicamente por los números reales no negativos.En general, el conjunto imagen siempre es un subconjunto del codominio, y cuando éstos coinciden, se dice que la función es suprayectiva
tiene por contra-dominio el conjunto de todos los números reales, pero como nunca toma realmente valores negativos, el conjunto imagen está formado únicamente por los números reales no negativos.En general, el conjunto imagen siempre es un subconjunto del codominio, y cuando éstos coinciden, se dice que la función es suprayectiva - RELACIÓN BINARIA
- Una relación binaria es una relación matemática
 definida entre los elementos de dos conjuntos
definida entre los elementos de dos conjuntos  y
y  . Una relación
. Una relación  de
de  en
en  se puede representar mediante pares ordenados
se puede representar mediante pares ordenados  para los cuales se cumple una propiedad
para los cuales se cumple una propiedad  , de forma que
, de forma que  , y se anota:
, y se anota: Que se lee: la relación binaria
Que se lee: la relación binaria es el conjunto de pares ordenados
es el conjunto de pares ordenados  tales que se vincula el primer elemento
tales que se vincula el primer elemento  propio del conjunto
propio del conjunto  con el segundo elemento
con el segundo elemento  propio del conjunto
propio del conjunto  , y para los cuales se cumple la propiedad
, y para los cuales se cumple la propiedad  que los relaciona.Las proposiciones siguientes son correctas para representar la relación binaria
que los relaciona.Las proposiciones siguientes son correctas para representar la relación binaria entre los elementos
entre los elementos  y
y  :
: También, según la notación polaca puede expresarse:
También, según la notación polaca puede expresarse: GRÁFICAS DE RELACIONES DE R EN R
GRÁFICAS DE RELACIONES DE R EN R - Por lo general, se usa cuando los conjuntos considerados son finitos y tiene pocos elementos.

- EJEMPLO
- (1) Sean A= {1,2,3} y B= {2,4,5,6} dos conjuntos, entonces las siguientes son relaciones entre A y B, por ser subconjuntos de AxB :

- FUNCIONES DE UNA VARIABLE REAL
- FUNCIÓN
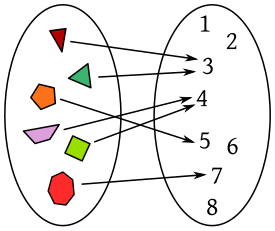
- Se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r2. Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.En análisis matemático, el concepto general de función, aplicación o mapeo se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):
... −2 → +4, −1 → +1, ±0 → ±0, +1 → +1, +2 → +4, +3 → +9, ... Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:..., Estación → E, Museo → M, Arroyo → A, Rosa → R, Avión → A, ... Esta es una función entre el conjunto de las palabras del español y el conjunto de las letras del alfabeto español.La manera habitual de denotar una función f es:- f: A → B
- a → f(a),
donde A es el dominio de la función f, su primer conjunto o conjunto de partida; y B es el codominio de f, su segundo conjunto o conjunto de llegada. Por f(a) se denota la regla o algoritmo para obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de B que le corresponde. En ocasiones esta expresión es suficiente para especificar la función por completo, infiriendo el dominio y codominio por el contexto. En el ejemplo anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:- f: Z → N
- k → k2, o sencillamente f(k) = k2;
- g: V → A
- p → Inicial de p;
si se conviene V = {Palabras del español} y A = {Alfabeto español}.Una función puede representarse de diversas formas: mediante el citado algoritmo o ecuaciones para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función. - La definición general de función hace referencia a la dependencia entre los elementos de dos conjuntos dados.Dados dos conjuntos A y B, una función (también aplicación o mapeo) entre ellos es una asociación f que a cada elemento de A le asigna un único elemento de B.Se dice entonces que A es el dominio (también conjunto de partida o conjunto inicial) de f y que B es su codominio(también conjunto de llegada o conjunto final).Un objeto o valor genérico a en el dominio A se denomina la variable independiente; y un objeto genérico b del dominio B es la variable dependiente. También se les llama valores de entrada y de salida, respectivamente. Esta definición es precisa, aunque en matemáticas se utiliza una definición formal más rigurosa, que construye las funciones como un objeto concreto.
- TIPOS DE FUNCIONES
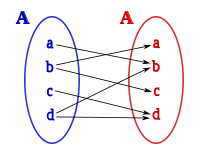
- FUNCIÓN INYECTIVA O UNO A UNO

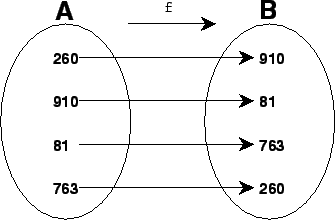
- Una función
 es inyectiva si a elementos distintos del conjunto
es inyectiva si a elementos distintos del conjunto  (dominio) les corresponden elementos distintos en el conjunto
(dominio) les corresponden elementos distintos en el conjunto  (codominio) de
(codominio) de  . Es decir, cada elemento del conjunto Y tiene a lo sumo una antiimagen en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.Así, por ejemplo, la función de números reales
. Es decir, cada elemento del conjunto Y tiene a lo sumo una antiimagen en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.Así, por ejemplo, la función de números reales , dada por
, dada por  no es inyectiva, puesto que el valor 4 puede obtenerse como
no es inyectiva, puesto que el valor 4 puede obtenerse como  y
y  . Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función
. Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función  entonces sí se obtiene una función inyectiva.
entonces sí se obtiene una función inyectiva. Definición formal
De manera más precisa, una función es inyectiva cuando se cumple alguna de las dos afirmaciones equivalentes:
es inyectiva cuando se cumple alguna de las dos afirmaciones equivalentes:- Si
 son elementos de
son elementos de  tales que
tales que  , necesariamente se cumple
, necesariamente se cumple  .
. - Si
 son elementos diferentes de
son elementos diferentes de  , necesariamente se cumple
, necesariamente se cumple 
Simbólicamente,que es equivalente a su contrarrecíprocoCardinalidad e inyectividad
Dados dos conjuntos y
y 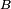 , entre los cuales existe una función inyectiva
, entre los cuales existe una función inyectiva  tienen cardinales que cumplen:
tienen cardinales que cumplen: Si además existe otra aplicación inyectiva
Si además existe otra aplicación inyectiva , entonces puede probarse que existe una aplicación biyectiva entre A y B.
, entonces puede probarse que existe una aplicación biyectiva entre A y B.- Si
- EJEMPLOS


FUNCIÓN SOBREYECTIVA

Una función  Es sobreyectiva (epiyectiva, suprayectiva, suryectiva, exhaustiva o subyectiva) si está aplicada sobre todo el codominio, es decir, cuando cada elemento de "Y" es la imagen de como mínimo un elemento de "X".
Es sobreyectiva (epiyectiva, suprayectiva, suryectiva, exhaustiva o subyectiva) si está aplicada sobre todo el codominio, es decir, cuando cada elemento de "Y" es la imagen de como mínimo un elemento de "X".
 Es sobreyectiva (epiyectiva, suprayectiva, suryectiva, exhaustiva o subyectiva) si está aplicada sobre todo el codominio, es decir, cuando cada elemento de "Y" es la imagen de como mínimo un elemento de "X".
Es sobreyectiva (epiyectiva, suprayectiva, suryectiva, exhaustiva o subyectiva) si está aplicada sobre todo el codominio, es decir, cuando cada elemento de "Y" es la imagen de como mínimo un elemento de "X".
Formalmente,

Cardinalidad y sobreyectividad
Dados dos conjuntos y
y 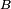 , entre los cuales existe una función sobreyectiva
, entre los cuales existe una función sobreyectiva  , se tiene que los cardinales que cumplen:
, se tiene que los cardinales que cumplen: Si además existe otra aplicación sobreyectiva
Si además existe otra aplicación sobreyectiva , entonces puede probarse que existe una aplicación biyectiva entre A y B.
, entonces puede probarse que existe una aplicación biyectiva entre A y B.- EJEMPLOS
- FUNCIÓN BIYECTIVA







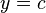



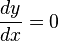
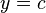
![Y =
\int_a^b c\,dx
\; \rightarrow \quad
Y =
c \; \int_a^b dx
\; \rightarrow \quad
Y =
c \; x \Big ]_a^b
\; \rightarrow \quad
Y =
c \; (b-a)](https://upload.wikimedia.org/math/9/1/7/91708e506c2ee42c07764057ed9e0176.png)

- Si
 es creciente en
es creciente en ![\left [ a,b \right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png)
- Si
 es decreciente en
es decreciente en ![\left [ a,b \right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png)
- Si
 es constante en
es constante en ![\left [ a,b \right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png)
- f es monótona.
- f tiene un límite por la izquierda y por la derecha en cualquier punto de su dominio de definición.
- f sólo puede tener discontinuidades de salto.
- f sólo puede tener una cantidad enumerable de discontinuidades.
- Si f es una función monótona definida en un intervalo I, entonces f es derivable casi siempre en I, es decir, el conjunto de puntos x en I en donde f no es diferenciable tiene medida de Lebesgue 0.
- Si f es una función monótona definida en un intervalo [a, b], entonces f es Riemann-integrable.

- FUNCIÓN PERIÓDICA
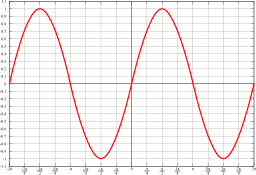

- Una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período, es decir:donde P es el período.De la misma manera, pero en un contexto físico, las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:
 donde el periodo propio fundamental
donde el periodo propio fundamental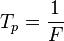 ,
,  es la frecuencia de la componente fundamental de la onda periódica y
es la frecuencia de la componente fundamental de la onda periódica y  un número entero.Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático).
un número entero.Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático). - FUNCIÓN PAR E IMPAR
- PAR

- Una función par es cualquier función que satisface la relación
 y si x es del dominio de f entonces -x también.Desde un punto de vista geométrico, una función par es simétrica con respecto al eje y, lo que quiere decir que su gráfica no se altera luego de una reflexión sobre el eje y.
y si x es del dominio de f entonces -x también.Desde un punto de vista geométrico, una función par es simétrica con respecto al eje y, lo que quiere decir que su gráfica no se altera luego de una reflexión sobre el eje y.Definición formal
El término función par suele referirse a una clase especial de funciones de variable real: una función es una función par si para
es una función par si para 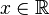 se cumple la siguiente relación:La definición anterior puede generalizarse a funciones sobre dominios más generales. Si A es un conjunto con cierta estructura algebraica en la que existan inversos aditivos (por ejemplo, los números complejos C), una función par sería toda función:que cumpla:La definición de función par presupone que si
se cumple la siguiente relación:La definición anterior puede generalizarse a funciones sobre dominios más generales. Si A es un conjunto con cierta estructura algebraica en la que existan inversos aditivos (por ejemplo, los números complejos C), una función par sería toda función:que cumpla:La definición de función par presupone que si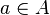 entonces necesariamente
entonces necesariamente  , de no ser así no se podría definir
, de no ser así no se podría definir  .
.Ejemplo
La función:es par ya que para cualquier valor de x se cumple:Demostrando que la función es par.Si x=2, entonces:
- IMPAR










- La única función que es tanto par e impar es la función constante que es idénticamente cero (o sea f(x) = 0 para todo x).
- La suma de una función par y una impar no es ni par ni impar, a menos que una de las funciones sea el cero.
- La suma de dos funciones par es una función par, y todo múltiplo de una función par es una función par.
- La suma de dos funciones impares es una función impar, y todo múltiplo constante de una función impar es una función impar.
- El producto de dos funciones pares es una función par.
- El producto de dos funciones impares es una función par.
- El producto de una función par y una función impar es una función impar.
- El cociente de dos funciones pares es una función par.
- El cociente de dos funciones impares es una función par.
- El cociente de una función par y una función impar es una función impar.
- La derivada de una función par es una función impar.
- La derivada de una función impar es una función par.
- La composición de dos funciones pares es una función par, y la composición de dos funciones impares es una función impar.
- La composición de una función par y una función impar es una función par.
- La composición de toda función con una función par es par (pero no vice versa).
- Toda función definida sobre toda la línea real puede descomponerse en la suma de una función par y una impar:
- La integral de una función impar entre -A y +A es cero (donde A es finito o infinito, y la función no posee ninguna asíntota vertical entre -A y A).
- La integral de una función par entre -A y +A es el doble de la integral entre 0 y +A (donde A es finito, y la función no posee ninguna asíntota vertical entre -A y A).
- Una función definida a trozos (también denominada función por partes, función seccionada o función definida por tramos) es una función cuya definición (la regla que define la dependencia), llamada regla de correspondencia, cambia dependiendo del valor de la variable independiente.Formalmente, una función real f (definida a trozos) de una variable real x es la relación cuya definición está dada por varios conjuntos disjuntos de su dominio (conocidos como subdominios).La palabra "A trozos" se usa para describir cualquier propiedad de una función definida a trozos que se cumple para cada trozo aunque podría no cumplirse para todo el dominio de f. Por ejemplo, una función es diferenciable a trozos si cada trozo es diferenciable a lo largo del dominio. En Análisis Convexo, la noción de la derivada puede ser reemplazada por la de subderivada para funciones definidas a trozos.
Definición
Si A y B son dos conjuntos cualesquiera y f una función definida entre ellos. Supongamos que A puede representarse como una unión de conjuntos disjuntos Ai
definida entre ellos. Supongamos que A puede representarse como una unión de conjuntos disjuntos Ai y que, para cada uno de los Ai, existe una función fi
y que, para cada uno de los Ai, existe una función fi Entoncesf es una función definida a trozos si
Entoncesf es una función definida a trozos si .En otras palabras, f es definida a trozos si su regla de asignación es diferente para al menos dos valores de la variable independiente.
.En otras palabras, f es definida a trozos si su regla de asignación es diferente para al menos dos valores de la variable independiente.Notación e interpretación
Las funciones definidas a trozos se expresan con una notación funcional común, donde el cuerpo de la función es una lista de expresiones matemáticas asociadas a subconjuntos del dominio.Por ejemplo, la función valor absolutopuede definirse asíEn este caso, el dominio fue dividido en los conjuntos los cuales son disjuntos y cumplen
los cuales son disjuntos y cumplen Para todos los valores de x menores que cero, la primera expresión matemática de la definición de abs(x) debe ser utilizada. Como esta expresión es –x, el signo del valor que asignamos a la variable independiente se invierte. De modo similar, para todos los valores de x mayores o iguales que cero, la segunda expresión matemática (la función x) es utilizada.A continuación, se presenta una tabla con valores de abs(x), en algunos puntos x del dominio.
Para todos los valores de x menores que cero, la primera expresión matemática de la definición de abs(x) debe ser utilizada. Como esta expresión es –x, el signo del valor que asignamos a la variable independiente se invierte. De modo similar, para todos los valores de x mayores o iguales que cero, la segunda expresión matemática (la función x) es utilizada.A continuación, se presenta una tabla con valores de abs(x), en algunos puntos x del dominio.x abs(x) Expresión utilizada −3 3 −x −0.1 0.1 −x 0 0 x 1/2 1/2 x 5 5 x En general, para evaluar una función definida a trozos en un determinado valor del dominio, seleccionamos la expresión matemática cuyo subdominio contiene el valor a evaluar.Continuidad
Una función definida a trozos es continua en un intervalo dado si está definida por el intervalo, las expresiones matemáticas apropiadas que constituyen a la función son continuas en ese intervalo, y no hay discontinuidad en ningún punto extremo de los subdominios en ese intervalo.La función que está a la derecha, por ejemplo, es una función definida a trozos continua en todos sus subdominios, pero no es continua en todo el dominio. Dicha función tiene un salto de discontinuidad (un agujero) en .
.
Una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
Formalmente, dada una función  :
:
 :
:
La función es biyectiva si se cumple la siguiente condición:
Es decir, si para todo  de
de  se cumple que existe un único
se cumple que existe un único  de
de  , tal que la función evaluada en
, tal que la función evaluada en  es igual a
es igual a  .
.
 de
de  se cumple que existe un único
se cumple que existe un único  de
de  , tal que la función evaluada en
, tal que la función evaluada en  es igual a
es igual a  .
.
Dados dos conjuntos  e
e  finitos, entonces existirá una biyección entre ambos si y sólo si
finitos, entonces existirá una biyección entre ambos si y sólo si  e
e  tienen el mismo número de elementos.
tienen el mismo número de elementos.
 e
e  finitos, entonces existirá una biyección entre ambos si y sólo si
finitos, entonces existirá una biyección entre ambos si y sólo si  e
e  tienen el mismo número de elementos.
tienen el mismo número de elementos.Teorema
Ejemplo
La función:
es biyectiva.
Luego, su inversa:
también lo es.1
El siguiente diagrama de grafos bipartitos se puede ver cuando la función es biyectiva:
| Funciones | Inyectiva | No inyectiva | ||
| Sobreyectiva |
|  | ||
| No sobreyectiva |  |  |
Cardinalidad y biyectividad
Dados dos conjuntos  y
y 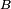 , entre los cuales existe una función biyectiva
, entre los cuales existe una función biyectiva  tienen cardinales que cumplen:
tienen cardinales que cumplen:
 y
y 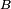 , entre los cuales existe una función biyectiva
, entre los cuales existe una función biyectiva  tienen cardinales que cumplen:
tienen cardinales que cumplen: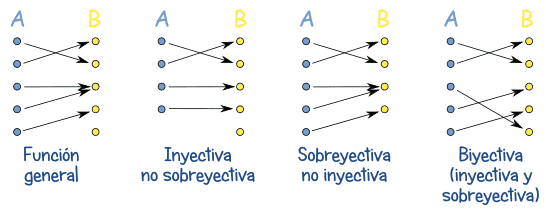
FUNCIÓN CONSTANTE
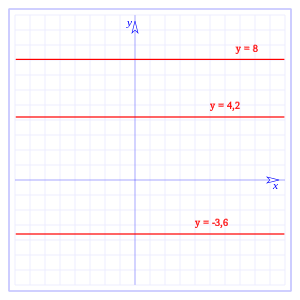
Se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable independiente. Se la representa de la forma:
Funciones reales de una variable real
Como se puede ver es una recta horizontal en el plano cartesiano, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
tenemos:
donde c tiene un valor constante, en la gráfica tenemos representadas:
Como la variable dependiente y no depende de x tenemos que:
la variación de y respecto a x es cero
La integral de la función constante:
es:
La función constante como un polinomio en x
Si un polinomio general, que tiene la forma:
una función constante cumple esta expresión con n= 0, es un polinomio de grado 0.
que es lo mismo que:
que corresponde al término independiente del polinomio.
FUNCIÓN CRECIENTE Y DECRECIENTE
Una función f es creciente es un intervalo si para cualquier par de números x1,x2 del intervalo. .
.
 .
.
Una fución f es decreciente es un intervalo si para cualquier par de números x1,x2 del intervalo,  .
.
 .
.
Sea f una función continua con ecuación y = f(x), definida en un intervalo [a,b]. La siguiente es la representación gráfica de f en el intervalo[a,b].
En la gráfica anterior puede observarse que la función f es:
1.) Creciente en los intervalos (a,x3),(x5,x6)
2.) Decreciente en los intervalos(x3,x5),(x6,b)
Criterio de crecimiento y decrecimiento
Sea f una función continua en el intervalo cerrado ![\left [ a,b\right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png) y derivable en el intervalo abierto
y derivable en el intervalo abierto  .
.
![\left [ a,b\right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png) y derivable en el intervalo abierto
y derivable en el intervalo abierto  .
.Ejemplo 1
Determinemos los intervalos en que crece o decrece la función con ecuación f(x) = 1 / 2(x2 − 4x + 1).
Para ello calculemos la primera derivada de f:f'(x) = x − 2.
Como f'(x) > 0 ↔ x − 2 > 0, o sea si x > 2, entonces f es creciente para x > 2.
Como f'(x) < 0 ↔ x − 2 < 0, o sea si x < 2, entonces f es decreciente para x < 2.
En la gráfica de la función puede observarse lo obtenido anteriormente.
Ejemplo 2
Determinar los intervalos en que crece o decrece la función f con ecuación f(x) = (x + 1) / (x − 1), con x ≠ 1.
La derivada de f es f'(x) = − 2 / (x − 1)2.
Como (x − 1)2es mayor que cero para x en los Reales, x ≠ 1, y además − 2 < 0entonces f'(x) < 0para todo x en los Reales (x ≠ 1), por lo que la función f es decreciente para x en los Reales, x ≠ 1 . La siguiente, es la gráfica de dicha función:
FUNCIÓN MONÓTONA
Definición general
Sea
una función entre dos conjuntos P y Q, donde cada conjunto tiene un orden parcial (los dos se denotarán por ≤). En cálculo se habla de funciones entre subconjuntos de losreales, y el orden ≤ no es otro que el orden usual de la recta real, aunque esto no es esencial para la definición.
La función f es monótona si y sólo si x ≤ y implica f(x) ≤ f(y) (es decir, la función es creciente), o bien x ≤ y implica f(x) ≥ f(y) (es decir, la función es decreciente). En otras palabras, una función es monótona si conserva el orden.
Monotonía en cálculo y análisis
En cálculo no hay usualmente necesidad de invocar los métodos abstractos de la teoría del orden. Como ya se señaló, las funciones se establecen entre (subconjuntos de) números reales, ordenados de forma natural.
Por la forma de la gráfica de una función monótona en los reales, tales funciones se llaman también monótonamente crecientes (o no decreciente), respectivamente.
Ejemplo gráfico
A continuación se muestran tres gráficas de funciones cualesquiera. La primera de ellas es una función estrictamente creciente por la izquierda y por la derecha, mientras que es constante en el medio; por lo demás, es creciente pues conserva el orden ascendente durante todo el recorrido de la función. La segunda de ellas es estrictamente decreciente por la izquierda y por la derecha, puesto que conserva el orden descendente durante todo el recorrido de la función. La última de ellas es una función con un recorrido con partes donde la función es creciente y partes donde es decreciente (presenta máximos y mínimos relativos).
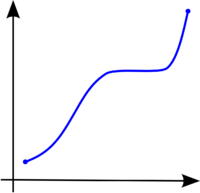 Función monótona creciente. | 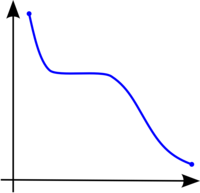 Función monótona decreciente. |  Función no monótona. |
Aplicaciones y resultados básicos
Monotonía En matemáticas, cada una de las siguientes propiedades de una función f : R → R implica la siguiente:
Estas propiedades son la razón por la que las funciones monótonas son útiles en el análisis matemático. Dos importantes hechos que se deducen de que una función sea monótona son:
Una importante aplicación de las funciones monótonas es en probabilidad. Si X es una variable aleatoria, su función de distribución
es una función creciente.
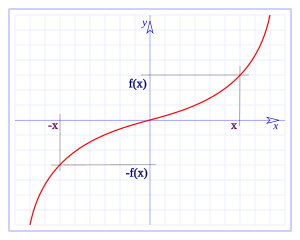
Una función impar es cualquier función que satisface la relación:
para todo x en el dominio de f.Desde un punto de vista geométrico, una función impar posee una simetría rotacional con respecto al origen de coordenadas, lo que quiere decir que su gráfica no se altera luego de una rotación de 180 grados alrededor del origen.Ejemplo
La función:
es impar, ya que:
en este caso la función no está definida en el punto  .
.
 .
.
Si vemos la función:
Podemos ver que:
Y esta función si pasa por el punto (0,0).
Características
Nota: La paridad de una función no implica que sea diferenciable o continua.
Propiedades


FUNCIÓN ACOTADA
ACOTADA SUPERIOR
FUNCIÓN LINEALES

En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:
- f(x) = mx + b
donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.
Algunos autores llaman función lineal a aquella con b = 0 de la forma:
- f(x) = mx
mientras que llaman función afín a la que tiene la forma:
- f(x) = mx + b
cuando b es distinto de cero, dado que la primera (b = 0) es un ejemplo también de transformación lineal, en el contexto de álgebra lineal.
Ejemplo
Una función lineal de una única variable dependiente x es de la forma:
- y = mx + b
que se conoce como ecuación de la recta en el plano x, y.
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:
- y = 0,5x + 2
en esta recta el parámetro m es igual a 1/2 (correspondiente al valor de la pendiente de la recta), es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el puntoy = 2.
En la ecuación:
- y = –x + 5
la pendiente de la recta es el parámetro m = –1, es decir, cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y = 5, dado que el valor de b = 5.
En una recta el valor de m se corresponde al ángulo θ de inclinación de la recta con el eje de las x a través de la expresión:
- m = tanθ
Funciones lineales de varias variables
Las funciones lineales de varias variables admiten también interpretaciones geométricas. Así una función lineal de dos variables de la forma
- f(x, y) = a1x + a2y
representa un plano y una función
- f(x1, x2, ..., xn) = a1x1 + a2x2 + ... + anxn
representa una hipersuperficie plana de dimensión n y pasa por el origen de coordenadas en un espacio (n + 1)-dimensional.
FUNCIÓN CUADRÁTICA

Una función cuadrática o función de segundo grado es una función polinómica definida por:
con  .1
.1
 .1
.1
Las gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vértice de la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 el vértice se encuentra en la parte superior, siendo un máximo (es decir, la parábola se abre "hacia abajo").
El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libreo el tiro parabólico.
La función derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.
Raíces
Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales  . Son denotadas habitualmente como:
. Son denotadas habitualmente como:  y
y  , dependiendo del valor del discriminante Δ definido como
, dependiendo del valor del discriminante Δ definido como  .
.
 . Son denotadas habitualmente como:
. Son denotadas habitualmente como:  y
y  , dependiendo del valor del discriminante Δ definido como
, dependiendo del valor del discriminante Δ definido como  .
.- Dos soluciones reales y diferentes si el discriminante es positivo,
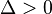 :
:
- Corta la parábola al eje X en dos puntos diferentes.
- Una solución real(o solución doble) si el discriminante es cero,
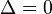 :
:
- La parábola es tangente al eje X.
- La parábola no corta al eje X.
- El único caso restante es que el discriminante sea negativo,
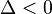 .
.
En tal caso, las raíces no son reales, sino que son dos números complejos conjugados:
Representación analítica
Hay tres formas de escribir una función cuadrática, aplicables según el uso que se le quiera dar a la función, un estudio analítico de la función o de la ecuación cuadrática, una interpretación o construcción geométrica de la parábola, etc.
Forma desarrollada o polinómica
La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito convencionalmente como:
con  .
.
 .
.Forma factorizada
Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como:
siendo a el coeficiente principal de la función, y  y
y  las raíces de
las raíces de  . En el caso de que el discriminante Δ sea igual a 0 entonces
. En el caso de que el discriminante Δ sea igual a 0 entonces  por lo que la factorización adquiere la forma:
por lo que la factorización adquiere la forma:
 y
y  las raíces de
las raíces de  . En el caso de que el discriminante Δ sea igual a 0 entonces
. En el caso de que el discriminante Δ sea igual a 0 entonces  por lo que la factorización adquiere la forma:
por lo que la factorización adquiere la forma:
En este caso a  se la denomina raíz doble, ya que su orden de multiplicidad es 2. Si el discriminante es negativo, las soluciones son complejas, no cabe la factorización.
se la denomina raíz doble, ya que su orden de multiplicidad es 2. Si el discriminante es negativo, las soluciones son complejas, no cabe la factorización.
 se la denomina raíz doble, ya que su orden de multiplicidad es 2. Si el discriminante es negativo, las soluciones son complejas, no cabe la factorización.
se la denomina raíz doble, ya que su orden de multiplicidad es 2. Si el discriminante es negativo, las soluciones son complejas, no cabe la factorización.Forma canónica
Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:
siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola.
Representación gráfica
Intersección con el eje y
La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):
lo que resulta:
la función corta el eje y en el punto (0, c), siendo c el término independiente de la función.
A este punto de la función también se lo conoce con Ordenada al Origen, ya que se da en los términos.
Intersección con el eje x
La función corta al eje x cuando y vale 0, dada la función
es decir:
las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión:
 .
.
Si la función no corta al eje x, la fórmula anterior no tiene solución (en los reales).
Extremo
Toda función cuadrática posee un máximo o un mínimo, que es el vértice de la parábola. Si la parábola tiene concavidad hacia arriba, el vértice corresponde a un mínimo de la función; mientras que si la parábola tiene concavidad hacia abajo, el vértice será un máximo.
Dada la función en su forma desarrollada:  , la coordenada x del vértice será simplemente:
, la coordenada x del vértice será simplemente:  . La coordenada y del vértice corresponde a la función f evaluada en ese punto.
. La coordenada y del vértice corresponde a la función f evaluada en ese punto.
 , la coordenada x del vértice será simplemente:
, la coordenada x del vértice será simplemente:  . La coordenada y del vértice corresponde a la función f evaluada en ese punto.
. La coordenada y del vértice corresponde a la función f evaluada en ese punto.
Dada la forma canónica:  , las coordenadas explícitas del vértice son: (h,k)
, las coordenadas explícitas del vértice son: (h,k)
 , las coordenadas explícitas del vértice son: (h,k)
, las coordenadas explícitas del vértice son: (h,k)
la derivada de la función, y se iguala a cero, la solución a esta ecuación son los posibles máximos y mínimos de la función, en este caso, partiendo de la función cuadrática:
calculamos su derivada respecto a x:
que si la igualamos a cero, tenemos:
donde x valdrá:
Para saber si es un máximo o un mínimo es necesario ver la derivada segunda de la función, veamos:
esto es: 2a será positivo cuando a sea positivo y negativo si a es negativo, por tanto, si la derivada segunda 2a es positiva la parábola es cóncava y el punto será un mínimo de la función, si a es negativa la parábola será convexa y sea un máximo.
Ejemplo 1
Dada la función:
Observación : Es indiferente notar "y" o notar "f(x)". Ambas expresiones hacen referencia a la imagen de x obtenida a través de la función trabajada.
Calculamos su derivada primera:
Esta derivada valdrá cero:
cuando:
esto es:
Esta función presenta un extremo relativo para  , veamos si es un máximo o un mínimo, calculando la derivada segunda:
, veamos si es un máximo o un mínimo, calculando la derivada segunda:
 , veamos si es un máximo o un mínimo, calculando la derivada segunda:
, veamos si es un máximo o un mínimo, calculando la derivada segunda:
Que es 6, dado que 6 es un valor positivo, la función es cóncava, y el extremo relativo que presente para:  , es un mínimo.
, es un mínimo.
 , es un mínimo.
, es un mínimo.
Obs. Observando el signo de la constante "a" podemos saber de antemano si estamos ante un mínimo o un máximo. Entonces para a<0 tendremos un máximo y para a>0 un mínimo.
Ejemplo 2
Dada la función:
Para calcular sus extremos relativos calcularemos su derivada primera:
Esta derivada valdrá cero cuando:
esto es:
que resulta:
Para  , la función presenta un extremo relativo, como sabemos que el coeficiente de
, la función presenta un extremo relativo, como sabemos que el coeficiente de  , es negativo es un máximo. Si realizamos el estudio de signo de la derivada primera, nos da que en
, es negativo es un máximo. Si realizamos el estudio de signo de la derivada primera, nos da que en  pasa de ser positivo a negativo, o sea la función cambia de ser creciente a decreciente, por lo que confirmamos que es un máximo. De otra forma; se puede calcular la derivada segunda en este punto, comprobando si la función es cóncava o convexa.
pasa de ser positivo a negativo, o sea la función cambia de ser creciente a decreciente, por lo que confirmamos que es un máximo. De otra forma; se puede calcular la derivada segunda en este punto, comprobando si la función es cóncava o convexa.
 , la función presenta un extremo relativo, como sabemos que el coeficiente de
, la función presenta un extremo relativo, como sabemos que el coeficiente de  , es negativo es un máximo. Si realizamos el estudio de signo de la derivada primera, nos da que en
, es negativo es un máximo. Si realizamos el estudio de signo de la derivada primera, nos da que en  pasa de ser positivo a negativo, o sea la función cambia de ser creciente a decreciente, por lo que confirmamos que es un máximo. De otra forma; se puede calcular la derivada segunda en este punto, comprobando si la función es cóncava o convexa.
pasa de ser positivo a negativo, o sea la función cambia de ser creciente a decreciente, por lo que confirmamos que es un máximo. De otra forma; se puede calcular la derivada segunda en este punto, comprobando si la función es cóncava o convexa.Otros procedimientos
- Si es posible factorizar en la forma
 , se halla el máximo del producto de los dos factores binómicos, teniendo en cuenta que
, se halla el máximo del producto de los dos factores binómicos, teniendo en cuenta que
tal caso ocurre si los factores son iguales, luego haciendo  se obtiene
se obtiene  o bien
o bien  .3 El signo de a determina si es mínimo o máximo.
.3 El signo de a determina si es mínimo o máximo.
 se obtiene
se obtiene  o bien
o bien  .3 El signo de a determina si es mínimo o máximo.
.3 El signo de a determina si es mínimo o máximo.- La forma canónica se puede escribir como
 , donde el segundo término conlleva un cuadrado, que es ≥ 0; pero en el segundo miembro si k/a es positivo, hay mínimo con x = h; si k/a es negativo, se obtiene un máximo si x = h.4 Todo ello para la función g(x)= 1/af(x).
, donde el segundo término conlleva un cuadrado, que es ≥ 0; pero en el segundo miembro si k/a es positivo, hay mínimo con x = h; si k/a es negativo, se obtiene un máximo si x = h.4 Todo ello para la función g(x)= 1/af(x).
Presencia
- En cinemática
en la ecuación del espacio en caso del movimiento uniforme acelerado: , donde a aceleración,
, donde a aceleración,  , velocidad inicial,
, velocidad inicial,  espacio inicial y t, variable del tiempo.,5
espacio inicial y t, variable del tiempo.,5
 , donde a aceleración,
, donde a aceleración,  , velocidad inicial,
, velocidad inicial,  espacio inicial y t, variable del tiempo.,5
espacio inicial y t, variable del tiempo.,5- En geometría
- En el área total de un cilindro, como función del radio de la base; de l modo en el área total del cono, en función del radio.

- En el área total de un prisma cuadrado, función del lado de la base, altura constante, lo mismo para la pirámide cuadrada.6
Presencia histórica[
Arquímedes calculó el área de un sector parabólico, limitado por un rectángulo, en términos modernos según la función  .7
.7
 .7
.7Determinar la ecuación conocidos tres puntos
Partiendo de la forma de la ecuación:
y conocidos tres puntos del plano xy por los que pasa una función polinómica de segundo grado:
se cumplirá que:
con lo que tenemos un sistema de tres ecuaciones con tres incógnitas, donde las incógnitas son: a, b y c, este sistema tendrá solución si el determinante de los coeficientes de las incógnitas es distinto de cero.
Representando el sistema ordenado de forma convencional:
Con lo que podemos calcular los valores de los coeficientes:
 |  |  |










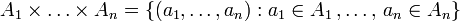

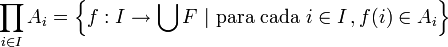
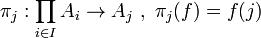
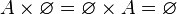
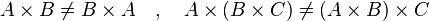
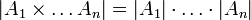
 , de los conjuntos
, de los conjuntos 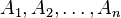 es un subconjunto del
es un subconjunto del 






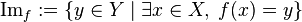


 es una
es una  existe y también es biyectiva.
existe y también es biyectiva.














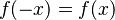





















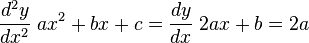







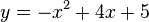


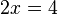



No hay comentarios:
Publicar un comentario